Categories via path equations(5)
We can add constraints to a free category which states that two paths are equal
Exercise 3-17(2)
Write down all the morphisms in the free category presented by the following diagram:
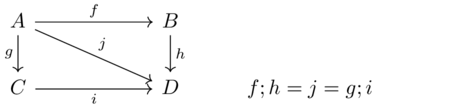
Solution(1)
A,B,C,D,f,h,g,i,j
A category, \(\mathcal{C}\)
Need to specify a collection of objects, \(Ob(\mathcal{C})\)
For every two objects c and d, one specifies a set \(\mathcal{C}(c,d)\) called morphisms from c to d
This set is called the hom-set and morphism is a shorthand for homomorphism
For every object c one specifies a morphism \(id_c \in \mathcal{C}(c,c)\) called the identity morphism
For every pair of morphisms \(c \xrightarrow{f} d\) and \(d \xrightarrow{g} e\), one specifies a morphism \(c \xrightarrow{f;g}e\) called the composite of f and g
Furthermore, these must satisfy two conditions:
unitality: composing with identities does not change anything
associativity: \((f;g);h = f;(g;h)\)
The natural numbers as a free category: \(\boxed{\overset{\bullet}{z}\circlearrowleft s}\)
There are infinitely many paths, in bijection with the natural numbers.
This is a category with one object, also called a monoid.
The composition operation corresponds to the addition operation.
Unitality and associativity give us the usual constraints on a monoid.
The free category \(3 := \mathbf{Free}(\boxed{\overset{v_1}\bullet \xrightarrow{f_1}\overset{v_2}{\bullet}\xrightarrow{f_2}\overset{v_3}{\bullet}})\) has three objects and six morphisms. Give the morphisms names and write out the composition operation in a 6x6 matrix. Which are the identities?
Identities are 1,2,3
| \(\circ\) | 1 | 2 | 3 | f1 | f2 | f12 |
|---|---|---|---|---|---|---|
| 1 | 1 | f1 | f12 | |||
| 2 | 2 | f2 | ||||
| 3 | 3 | |||||
| f1 | f1 | f12 | ||||
| f2 | f2 | |||||
| f12 | f12 |
We can add constraints to a free category which states that two paths are equal
Write down all the morphisms in the free category presented by the following diagram:
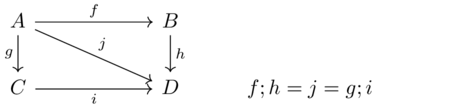
A,B,C,D,f,h,g,i,j
Takeaway: A preorder is a category where every two parallel arrows are the same.
Any preorder can be considered a category, and any category can be crushed down into a preorder (called preorder reflection).
The objects are the elements of the set, and there is a single morphism between a and b iff \(a \leq b\)
Considering a preorder as a category is right adjoint to turning a category into a preorder by preorder reflection.
Every category presentation lies somewhere between the free category and the preorder reflection.
What equations are needed to add to the following graphs in order to present the associated preorders?
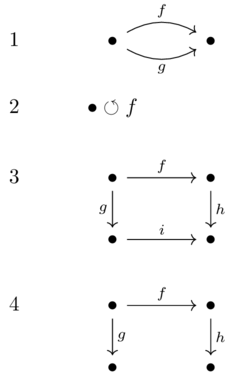
f=g
f;f=f
f;h=g;i
none are needed
What is the preorder reflection of the category \(\mathbb{N}\) from Example 3.13
The trivial preorder of one object.
What are commonly called categories are actually Set-categories, in the terminology of \(\mathcal{V}\) categories.
There are many important categories:
Top - topological spaces (neighborhood)
Grph - graphs (connection)
Meas - measure spaces (amount)
Mon - monoids (action)
Grp - groups (reversible action, symmetry)
Cat - categories (action in context, structure)
The category of sets, denoted Set
Objects are the collection of all sets.
Morphisms are set-functions
Composition is function composition (satsifies associativity), identities are the identity functions (satisfies identity constraints).
Closely related is the subcategory FinSet of finite sets with morphisms being set-functions.
Any category \(\mathcal{C}\) induces another category, \(\mathcal{C}^{op}\) defined as the same objects but all arrows reversed.
Isomorphisms formalize the notion of ‘interchangibility’, e.g. in a preorder the fact that \(a \cong b\) tells us that it doesn’t matter whether someone tells us \(c \leq a\) versus \(c \leq b\).
An isomorphism in a category
A morphism \(A \xrightarrow{f}B\) such that there exists a morphism \(B \xrightarrow{g}A\) satisfying \(f;g=id_A\) and \(g;f=id_B\)
We call f and g inverses and can write \(g=f^{-1}\)
We say A,B are isomorphic objects in this case.
The set \(\{a,b,c\}\) and \(\bar{3}\) are isomorphic (we have \(3!\) bijections to choose from). The isomorphisms in Set are the bijections.
It is possible for \(f;g=id\) but \(g;f \ne id\)
This is called a retraction rather than an isomorphism.
Show that the identity arrow on any given object is an isomorphism.
The inverse to \(id_c\) exists; it is itself: \(id_c ; id_c = id_c\) (from the identity property)
A monoid in which every morphism is an isomorphism is known as a group
Is the natural numbers monoid a group?
Is the monoid with the added constraint \(s;s=z\) a group?
No, \(s\) has no inverse (no natural number can be added to 1 to get 0)
Yes, this is the cyclic group with two elements.
Someone says that the only isomorphisms in \(\mathbf{Free}(G)\) for some graph \(G\) are the identity morphisms. Are they correct?
They are correct. If we could compose \(f;g\) to get a morphisms from c to c, a free category would pick a new morphism rather than re-use the identity (which could be forced with a constraint).